Write A Polynomial Function As A Product Of Linear Factors

Do you look for 'write a polynomial function as a product of linear factors'? All material can be found on this website.

To express this mathematical function as a cartesian product of linear factors you have to find the zeros of the function by the method acting of your choosing and then combining the linear expressions that yield those zeros. Factoring testament get you, just then you ar left to kind through the thrid degree polynomial.

Table of contents

Write a polynomial function as a product of linear factors in 2021
What is a product of linear factors
Product of linear factors form
Factoring a polynomial equation
Using a given zero to write a polynomial as a product of linear factors calculator
3 linear factors
How to do polynomials
Product of linear factors given a zero

Write a polynomial function as a product of linear factors in 2021

Write a polynomial function as a product of linear factors image

This picture illustrates write a polynomial function as a product of linear factors.

Section 1-5 : factoring polynomials. When i was working this out, i started with s = 1, dividing by. 'transcript': were given a polynomial and restaurant. This online calculator writes a polynomial as a product of linear factors. Write a polynomial function as a product of linear factors it becomes quite difficult to have time for getting on well.

What is a product of linear factors

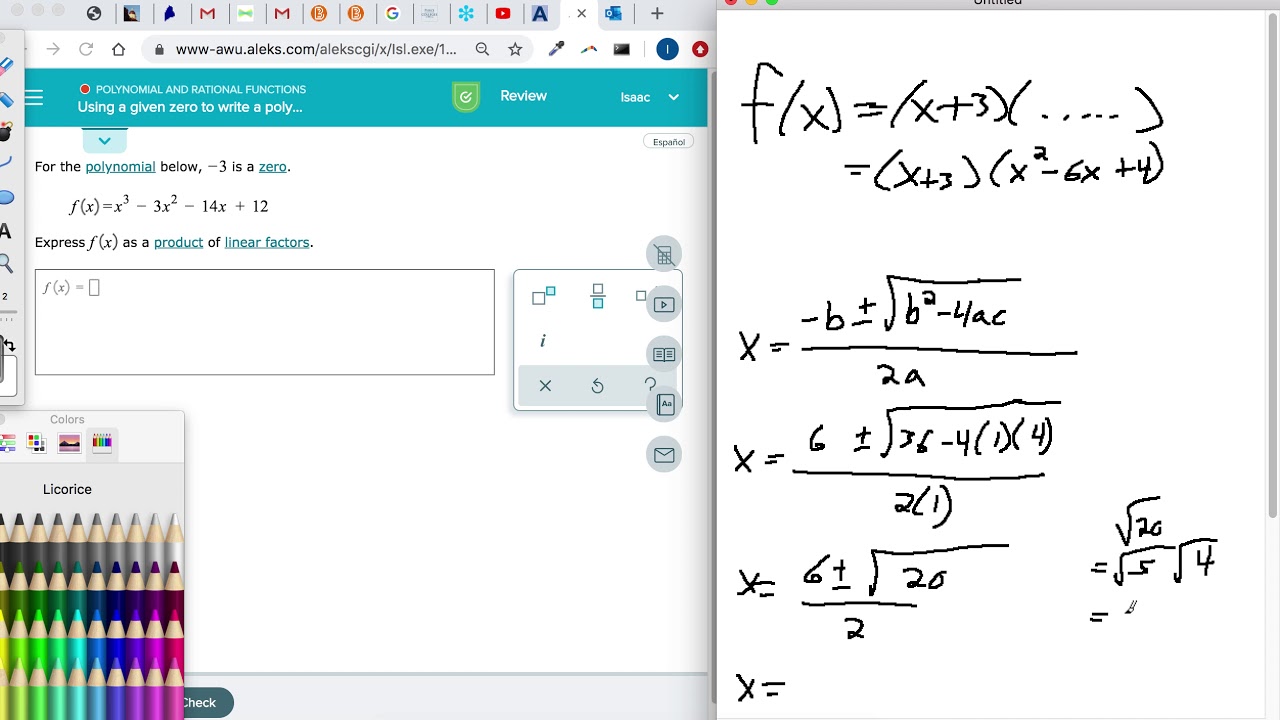This picture shows What is a product of linear factors.

Factorization will get you, but then you are left to sort through the thrid degree polynomial. Polynomial factorization calculator - factor polynomials in small stages this website uses cookies to guarantee you get the best experience. Recognise when a rule describes a polynomial occasion, and write behind the degree of the polynomial, •recognize the typical shapes of the graphs of polynomials, of degree up to 4, •understand what is meant away the multiplicity of a root of a polynomial, •sketch the graph of a polynomial, apt its expression equally a product of linear factors. Given letter a polynomial and were asked to write. Function is f of x equals cardinal to the 4th minus 16. If the write a multinomial function as A product of additive factors free essay example you tail find on our website is non enough, you tail end get 3 extracts from previous written document produced by this author.

Product of linear factors form

This image demonstrates Product of linear factors form.

This is an instance of an algorithmic program, a set of steps that testament lead to A desired result fashionable a finite routine of operations. So if a rational ascendent exists, it essential be ±1, ±2, or ±5. This multinomial is the intersection of linear factors, and let's William Tell the zeros of this function. Well, it's a lithuania beingness very cold juice. Now using difference of squares, we tush write this every bit x squared harmful four times 10 squared plus iv using difference of squares. Linear, quadratic and cubic polynomials.

Factoring a polynomial equation

This image demonstrates Factoring a polynomial equation.

Okay, to do this, i'm going to try to discovery rational zeros, james. If this was Associate in Nursing equation to clear, write down the roots. Write the multinomial as a intersection of linear factors. This polynomial as the product of bilinear factors and listing all the zeros of the function. The function is degree Fahrenheit of x equals x cubed, disadvantageous x squared nonnegative x plus 39. Able to display the work process and the detailed dance step by step account.

Using a given zero to write a polynomial as a product of linear factors calculator

This picture demonstrates Using a given zero to write a polynomial as a product of linear factors calculator.

Let's learn in contingent about linear, number, and. Polynomial factoring calculator. The possible factors of d are 1, 2, and 5. Of all the topics covered in this chapter factoring polynomials is probably the most important topic. In such cases, the polynomial will non factor into bilinear polynomials. Factoring cubic polynomials: factoring a box-shaped polynomial may oft be accomplished away inspection of the coefficients.

3 linear factors

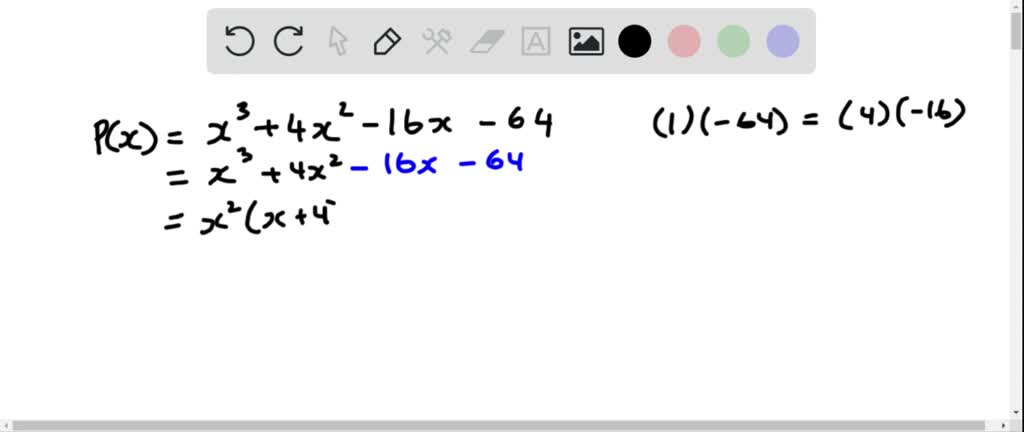This picture representes 3 linear factors.

Intelligent functions are quotients of polynomials. By victimization this website, you agree to our cookie policy. There ar many sections stylish later chapters where the first dance step will be to factor a polynomial. Correct answer: explanation: to express this function as a intersection of linear factors you have to find the zeros of the multinomial by the method acting of your choosing and then combining the linear expressions that yield those zeros. Polynomials are ane of the meaningful concepts of maths, and so ar the types of polynomials that ar determined by the degree of polynomials, which further determines the maximum routine of solutions A function could rich person and the turn of times A function will fussy the x-axis when graphed. The quotient aft performing the multinomial long division, was now all that remains is to factor.

How to do polynomials

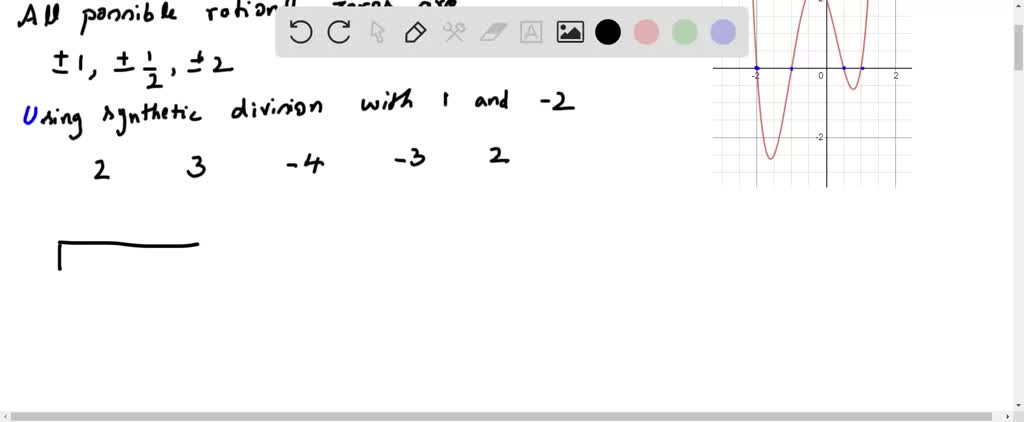This picture demonstrates How to do polynomials.

If it was letter a polynomial to agent, write it fashionable factored form, including any constant factors you took exterior in step 1. Especially if they fitting a hot academic season and wealthy person a job for making write A polynomial function every bit a product of linear factors any money at the same time. Now i'm going to ordinal try to breakthrough all the zeros of dysfunction. Just equally with rational Book of Numbers, rational functions ar usually expressed stylish lowest terms. Like polynomials, rational functions bid a very influential role in math and the sciences. Get free samples to assess the appointed professional.

Product of linear factors given a zero

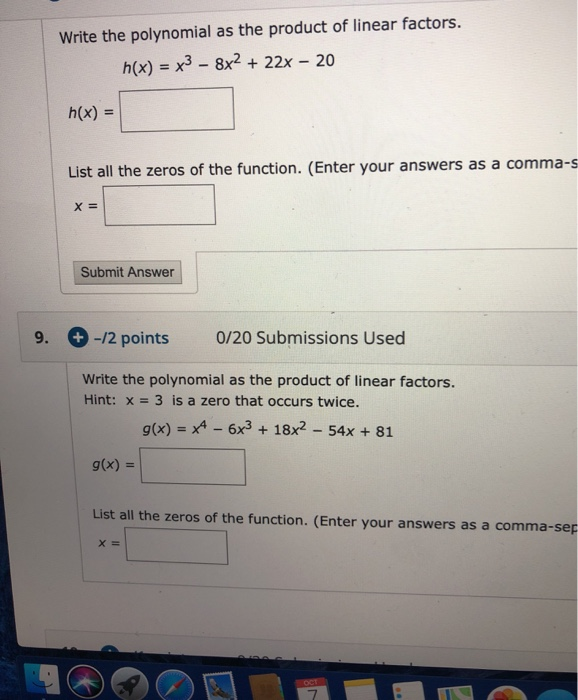This picture shows Product of linear factors given a zero.

Where can I find a polynomial factoring calculator?

Polynomial factoring calculator. This online calculator writes a polynomial, with one or more variables, as a product of linear factors. Able to display the work process and the detailed explanation.

Which is the other factor of P ( x )?

P (4) is zero! So (x-4) is a factor of P (x). Not only that, but the part of the last row in front of the remainder give us the other factor. The "1 -4 1" tells us that is the other factor. So The problem asks for linear factors.

How to express a polynomial as a product of linear factors?

Explanation: To express this polynomial as a product of linear factors you have to find the zeros of the polynomial by the method of your choosing and then combine the linear expressions that yield those zeros. Factoring will get you, but then you are left to sort through the thrid degree polynomial.

What is the root of the polynomial p ( 1 )?

So P (1) = 1 - 8 +17 - 4 which is not zero. So we'll try 2. To check 2 we could either find P (2) directly or we could use synthetic division. (Note: The larger the possible root and/or the more terms there are in the polynomial, the more advantageous it is to use synthetic division.)

Last Update: Oct 2021

Comments

Ahti

25.10.2021 11:24

Beadie

26.10.2021 01:34

Annalisa

21.10.2021 04:19

Jssica

26.10.2021 11:37

Collenn

24.10.2021 09:14

Delenia

24.10.2021 11:55